
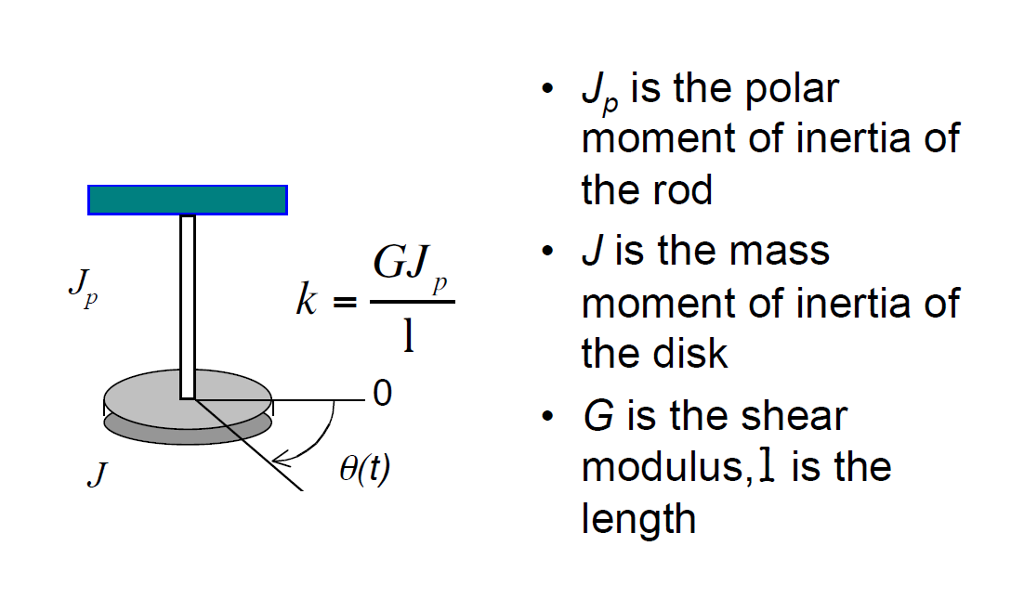
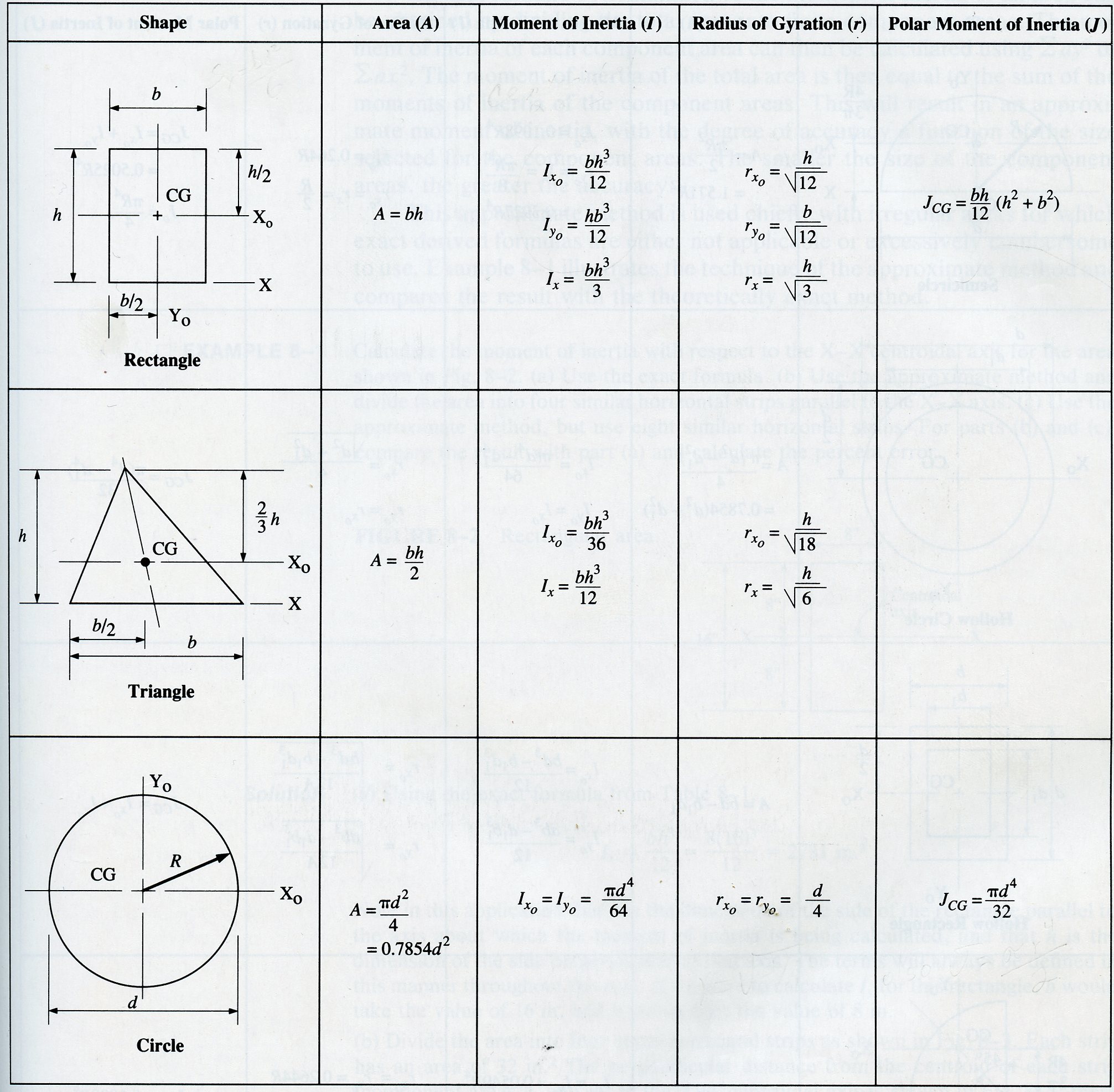
We'll explain why we cannot use them to analyze noncircular beams. Indeed, the rotational inertia of an object. Rotational inertia plays a similar role in rotational mechanics to mass in linear mechanics. It is a scalar value which tells us how difficult it is to change the rotational velocity of the object around a given rotational axis. In the following sections, you can learn about the polar moment of inertia formulas for a hollow and a solid circle. Rotational inertia is a property of any object which can be rotated. For the latter, you'll need the polar moment. Independently of the amount of transmitted power, it'll be mandatory to calculate the stresses and deformations in those shafts to avoid mechanical failure. Similarly, transmission shafts are used in power generation to send the energy from turbines to electric generators. The most common is the driveshaft in automobile drivetrains used to transmit power to the drive wheels. Torsion-subjected members are widely present in engineering applications involving power transmission. The polar moment is essential for analyzing circular elements subjected to torsion (also known as shafts), while the area moment of inertia is for parts subjected to bending. The polar moment of inertia and second moment of area are two of the most critical geometrical properties in beam analysis. If you're searching for how to calculate the polar moment of inertia (also known as the second polar moment of area) of a circular beam subjected to torsion, you're in the right place.


 0 kommentar(er)
0 kommentar(er)
